EMPbridge团队在重叠网格界面自适应法求解运动涡流场问题方面取得进展

含运动导体的涡流场计算是一个具有挑战性的问题。导体移动使得原始网格发生变形，进而要求重新网格剖分，对于具有复杂几何形状的工程模型，网格剖分非常耗时。为此，EMPbridge团队提出一种基于重叠非协调网格界面自适应的网格划分方法，并在不改变背景网格拓扑结构的情况下，将入侵界面转化为运动部件之间的非协调界面，避免了生成小的或不规则的切割单元。

基于重叠网格的数值算法放宽了对网格的要求，可以处理任意形式的运动和变形，但由于背景网格是固定不变的，运动网格的界面会侵入背景网格单元的内部。有必要根据侵入界面的位置和形状在两部分网格的自由度之间建立约束。EMPbridge团队提出在不改变背景网格拓扑结构的前提下，将入侵界面转化为单元间的非协调界面（如图1），并在此基础上求解非协调网格的涡流场问题。

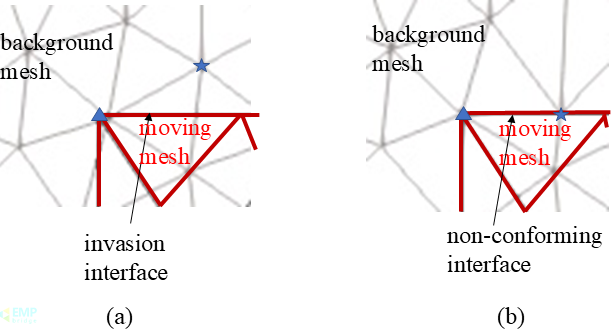
图1 侵入界面(a)和不协调界面(b)，三角形和五角星用于标记网格位置更改节点。

非协调界面重构步骤如下：

(1)选择围绕运动导体的多边形区域作为运动域，分别对背景区域和运动区域进行网格划分，得到初始网格，如图2a所示。

(2)对每个计算时步，根据新位置在背景域上进行运动域的几何界面重建，得到背景网格在运动区域上的投影网格，如图2b所示。

(3)选择运动区域的初始网格或背景网格在运动区域上的投影网格作为当前网格，通过网格映射处理运动区域投影网格中背景网格的自由度，求解运动电磁场问题。如图2c和2d所示。

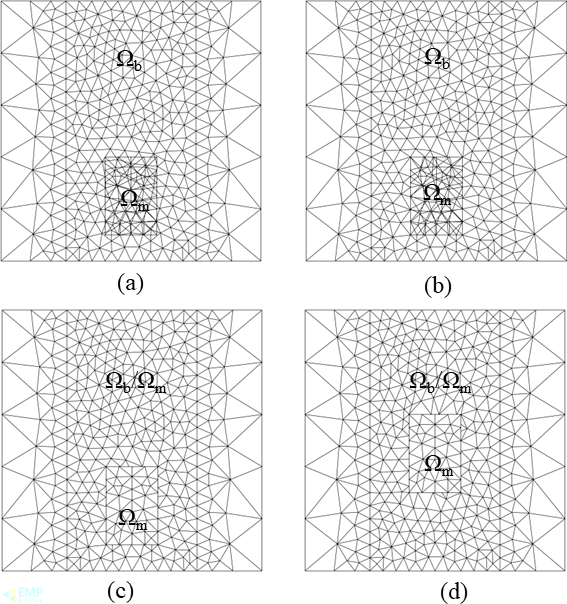
图2界面自适应过程描述

团队通过自由空间中移动导线示例验证了算法的准确性。

其几何模型、局部网格和磁通密度分布结果分别如图3、图4所示。两种方法在相对粗网格（网格1）和相对细网格（网格2）上的数值误差结果见图5。结果表明所提方法有效保持了求解精度。

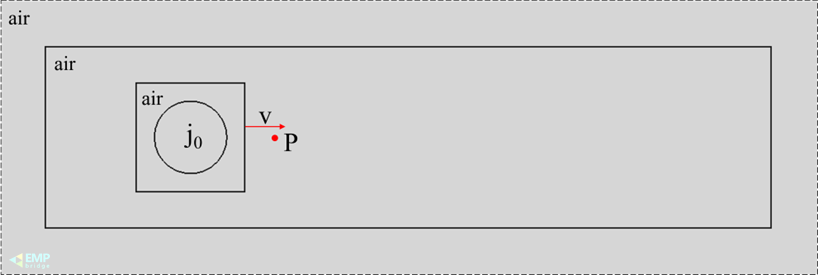
图3 空间中运动导线的几何模型

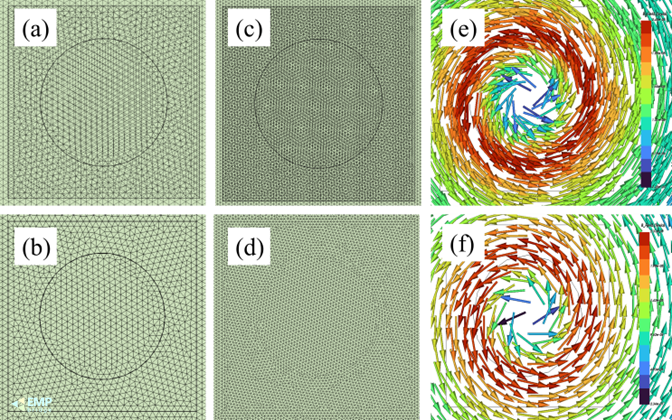
图4 局部网格：(a)所提方法网格1，(b)所提方法网格2，(c)网格重剖法网格1，(d)网格重剖法网格2，(e)网格1磁通密度分布，(f)网格2磁通密度分布

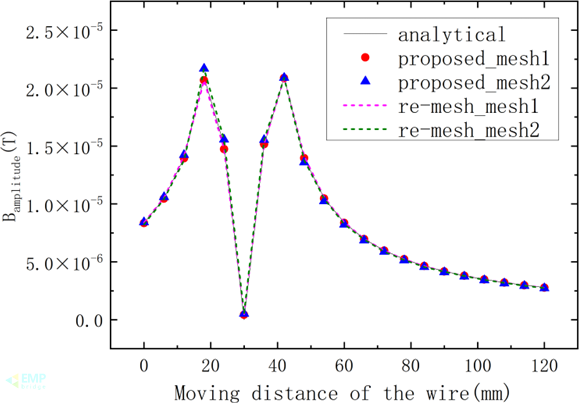
图5 点P在两种方法的两种网格下磁通密度计算结果对比

团队研究分析了一个永磁体悬浮装置算例。其几何模型如图6所示，0.16 s (图7(a)) 和0.8 s (图7(b))两个时刻的磁矢量位场等势线和涡流场分布如图8所示。

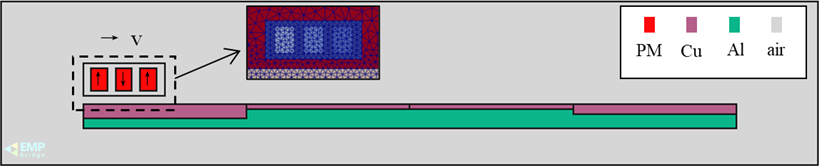
图6 算例几何模型、局部网格以及材料

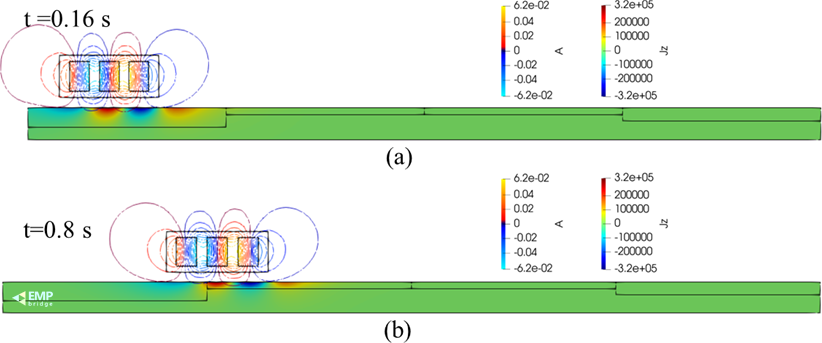
图7 不同时刻的磁矢量势(A)和涡流密度(Jz)分布

所提出的方法大幅减少计算时间，主要技术优点有：1）支持多自由度运动，在运动形式和运动范围上具有更大的灵活性；2）运动过程中保持了相同的自由度结构；3）考虑了端部效应。

上述计算基于自主研制的多物理耦合仿真软件平台EMPbridge实现。

相关成果以“Computation of Movement Involved Eddy Current Field Using Interface Adaptation of Overlapping Mesh”为题，在国际知名学术期刊IEEE Transactions on Magnetics发表，DOI：10.1109/TMAG.2024.3498098。